In the Fullness of Time

It was a He-Man action figure, I think, that started the trouble on that spring day early in my teaching career. If you're old enough to remember they heyday of He-Man and his, um, business associates (the name Skeletor ring a bell?), congratulations. (And you do need to have some age on you, as these figures were popular in my kindergarten classroom around the same time as the A-Team and just before Cabbage Patch Kids (bless their ***** little hearts) and Transformers.) If you're not old enough to remember the excitement, if you grew up outside the cultural influence of the USA, or if your memory is like a sieve, never mind. It was a toy, that's all you need to know; a coveted toy, a toy with a definite cool factor, the kind of toy that conferred automatic social standing on its owner, even in kindergarten.

Anyhow, there was a stray He-Man figure, a slightly dusty one that someone had found wedged halfway under a shelf near the block corner. He immediately claimed it as his own property, based on two incontrovertible legal principles (incontrovertible among five-year-olds, at least): first, he'd found it; and second, just in case that didn't carry any weight with others, he was almost certain he'd lost that very figure some time earlier, and lost it in a part of the room that was surprisingly near the shelf in question. At first no one challenged the incontrovertibility of these claims, and he was happily showing it off to all his friends, and growing no doubt in social standing all the while...when up came another child, who promptly rocked the boat by claiming this very He-Man as his own property.

It soon became apparent that this was going to be one of those situations: a he-said, he-said situation, long before Anita Hill and Clarence Thomas came along to popularize that expression, or one almost exactly like it. A glance at the toy in question was of no help in resolving ownership. One He-Man toy looked very like another, after all, extruded as they were from the same plastic molding machine and colored by the same shade of dyes, and other than the dust there were no particular marks that distinguished this particular figure as belonging to either of the boys. No parent had scrawled his or her child's initials on the figure's lower back; no child had affixed a slice of black tape to He-Man's mighty foot for easy recognition; no serial numbers appeared on He-Man's warrious helmet.

"It's mine," said one of the boys, lower lip trembling, "I know it is. I remember."

"It's mine," said the other boy, a catch in his voice. "I recognize it."

Both looked pleadingly at the adult, a.k.a me. A Solomonic situation, I remember thinking, and briefly toyed with the notion of threatening to cut the figure in half. But no, I ducked, and simply suggested that they try to work out a fair way to solve the problem. That, after all, was high on the list of values at the school, the ability to talk about problems and come to an agreement that would be, um, agreeable to both parties. (I note here that few of my former students seem to have gone into politics.) "Take a few minutes," I said, "talk about it, see what you come up with. When you have a plan that you think will work, let me know."

Off they went. And a few minutes later they were both back. The quivering lower lip was still, the tremor in the voice had ceased. "We worked it out," they told me in unison. And they had. "First I get it for ten years..." said the boy who had found it below the shelf.

"And then I get it for ten years," added the other boy.

It was a fair deal, on its surface, but I couldn't help feeling there was a flaw in their plan somewhere or other...

In Which the Math Guy Is Reminded (Yet Again) of the Importance of Not Making Assumptions

The second graders were measuring. They'd cut out replicas of their feet (exact size, natch) and were busily determining how many of these footprints (feetprints?) it took to equal the length of a shelf, the width of the room, and other various and sundry distances. Then they were converting the number of feetprints (footprints?) to inches and recording it all on a chart.

I plunked myself down next to a child who was recording the number of feetsprint she had needed to cover the distance across a table. She'd written a 7, which sounded reasonable--seven second-grade-sized footsprint looked about right--but what was this next to it? A zero? Seventy? Surely she was putting 70 in the wrong place of the chart. Or she'd mismeasured. Or--
Wait a minute.

It wasn't just a zero. It was a bubble letter--you know, the puffy letters that kids love to make, especially when time is of the essence. The ones that slow kids' work pace down to a crawl. The ones that drive me faintly crazy. The ones that--

Hold on.

Now she was decorating the thing. Shading in part of the inside ring, drawing something unrecognizable in the middle. Decorating--during math time! Bubble letters--during math time! I mean, gee whillikers!

I opened my mouth to say something gentle, yet pointed. Okay, something not-so-gentle yet pointed. Something about saving the artistry for art and getting back to math, and by-the-way was 70 really a reasonable answer, and if you'd been paying closer attention to the math rather than to the art you'd know...But then I didn't. "Tell me about what you're drawing," I said instead, pointing. Just in case my assumption was wrong and there was method to her madness.

"Oh, that's a quarter," she explained, barely looking up.

"The coin?" I asked. "The thing that's worth twenty-five cents?" I peered closer. Okay, now that she'd mentioned it I could see that the bubble-letter zero did indeed resemble a quarter. Fine and dandy, but that didn't explain why she drawn a coin as part of this measurement project. I opened my mouth again...but instead of the pointed comment I'd intended, I found myself with a different response, again a response that didn't automatically assume that she'd messed up.

"Why a quarter?" I asked.

"Well," she said, "when I measured the table I found it was seven and a quarter of my footsprints." She tapped the seven on the chart, then the quarter beside it. "So I wrote seven, and then I drew a quarter. That's why."

And that's why I'm glad I asked!

at10tion!

Yup, it's the day we've all been waiting for--at least, the day us Math Guys have all been waiting for: Ten Ten Ten, or 10/10/10. (As many of you Eager Readers no doubt know, 10 holds a special place in every math guy's heart. 2 1/2, 8, 92, 753.6, even 3.14159...., they all have their points (some of them even have decimal points (sorry)), but none of them can hold their own next to Ten.) However you write it, it's as decimal a day as it gets (well, okay, 10/10/1010, a thousand years ago this afternoon, was maybe a skoonch better, and there's something quite appealingly, I don't know, clean, about 10/10/10 back in 10 CE, not that anyone knew it WAS 10 CE at the time).

I had a distant relative who I met back in 1978 or so. She showed me her passport and called my attention to her birthdate. I know, I know, ladies of a certain age are not supposed to reveal their ages, but she was so pleased with the day she was born that she couldn't resist. It was, of course, 10/10/10--1910, that is. I promised not to do the subtraction necessary to calculate her age at the time. Here's to you, Cousin Lily.

So have a happy Ten Ten Ten. Ten cheers for this day, and long may it wave.

Or We Could Just Call 'em Number Cube(s)

First grade, a lesson on estimation.

"I'm going to show you a cup with dice inside," I explained. "I won't show it for very long. So, you won't be able to count how many there actually are. Instead, I want you to decide how many it COULD be and how many it COULDN'T be. Got it?"*

*The purpose of this activity is to get kids to establish a zone of possible answers. Very often kids think of estimation as a sport in which the goal is to guess exactly the right answer. It isn't. This project asks kids to identify numbers that they think are reasonable. The zone can be quite large (when working independently later on, one partnership ruled out 1, 2, 3, 4, and 5, and decided that anywhere from 6 up to 40 was perfectly reasonable) or quite small (another pair, in direct contrast, established a zone that went all the way from 10 to 11). Either way, you get a sense of kids' ability to think about large quantities and a sense of the confidence (or overconfidence) they bring to the table when it comes to mathematical thinking.

"Okay," I said when everyone had taken a look. "Would you say the cup is full?"

NO, they chorused. Some said it was mostly empty, others about half full, but all agreed that it absolutely was not full or even close.

"Could you see all the dice at the same time?" NO, again.

I had a number line of sorts on the board. I touched the number 1. "Could there be just one object in the cup?" I asked. NO. "How about 2?" NO. "Three?" NO, NO, NO. "Okay," I challenged, because after all explaining your thinking is an important part of mathematics, "you sound awfully sure. How can you be so sure?"

A boy raised his hand. "I could see if it was three," he said, holding up three fingers. "I couldn't tell how many there were, so I knew it wasn't more than three." He could tell just by looking, because he knew what three looked like. A couple of other children followed by explaining their own reasoning in remarkably similar terms. Great minds and all that.

One child remained with her hand up. "Yes?" I asked.

She smiled. "I knew it couldn't be just 1," she said, "because you said you had dice in the cup, and if there was just one then you would have to say you had a die in the cup."

True, too!

You're Wrong HA HA HA

Ellen asked her 4th graders to write down what helped them in solving math problems, and what did precisely the opposite. This is a great assignment, as it requires kids to think about their own study habits and student skills: metacognition at its finest.

It was also fun to read the replies. Most students said that a quiet room helped. (More students, it strikes me, than there are students who actually help KEEP the room quiet, but it's the thought that counts.) Many said that having manipulatives to work with was helpful. And a few were very specific: What helps, wrote one student, is "people keeping their feet to themselves."

More interesting, however, were the things that children said did NOT help. Here they were usually quite detailed and focused in their complaints.

It makes it hard, said one child, when "people [are] invading my personal space." (Presumably that includes invading it with feet; see above.)

"Being told that your idea is terrible," suggested a classmate.

"When people are unnice," commented a third. (I agree. I much prefer it when people are unmean. Not to mention unloud.)

Another student wrote: "To hear any bragging or any kind of DISTRACTION." [caps in the original]

Another hated hearing "I wish you'd catch up with me so we can work together, since I'm so much farther than you." (A subtle slam, couched in nice enough words but with a very unnice message.)

"To say 'I'm right and you're wrong HA HA HA," wrote another student. (Bad enough to be wrong, worse for someone else to be right, but I agree, the HA HA HA really puts it over the edge into no-jury-would-ever-convict territory.)

And this one, which sounds like a couple of lines from a 50s song, maybe sung by one of those girl groups I can never remember the name of:

"I don't like to be pressured
I don't wanna be bugged."

(If you'd like to take a stab at completing the lyric, please note that "pressured" rhymes nicely with "Eschered"--presumably the act of being turned into an impossible figure or a slightly bizarre tessellation--and "bugged" with "hugged," "chugged," "plugged," "tugged," and "mugged." Among others. Good luck!)

The World Cup, Plus Math

Yes, I have been following the World Cup tournament. Though I cannot say I know all that much about soccer, I appreciate the "beautiful game" as much as anyone in my knowledge range. I particularly enjoy beautiful things like, oh, the delightful drone of the airhorns, the charming attempts by France's media, athletes, and managers to blame everybody else for the French team's insipid play, and the ever-admirable arguments over the eyesight, credibility, and integrity of various officials. And the goals are pretty cool too. (Though I have to say that as a one-time [very low-level] water polo goalie I appreciate some of those saves even more. Man oh man alive, the things those guys can do...]

But what attracts us Math Guys to the World Cup, of course, isn't flags, or controversy, or those funky yellow shoes the Honduras players are wearing. No, the real draw, OB-viously, is the mathematics of the tourney. There really are a lot of interesting mathematical puzzles and problems surrounding the World Cup, and on the chance that your child--or you yourself--might be interested in a few World Cup Math Queries, here's your chance.

Some background: In the first round, teams are divided into groups of 4. Each team plays each other team in its group once, for a total of 3 games. You get 3 points for a win, 0 points for a loss, and 1 point for a tie.

A warm-up or two first.

Question 1. What is the greatest number of points a team can get during the first round of the tournament?

Question 2. What is the fewest number of points a team can get during this round?

Too easy? All right. Here's a slightly harder one.

Question 3. A team can get various single-digit point totals during the first round. For instance, 2 ties will result in 2 points. However, there is one single-digit point total that a team canNOT get during this round. What is it?

Question 4. If I told you my team finished round 1 with just 1 point, you'd be able to tell me its record. (You'd also be able to tell me my team was going home.) What would its record be? That is, how many wins, how many losses, how many ties?

Question 5. There's one point total, though, that's ambiguous. That is, there are two possible won-loss-tie records that will result in that number of points. What is that total? And what are the two different records that will get you there?

I alluded a couple of questions ago to the fact that some teams GO HOME. Yes. Only the top two teams from each group survive to play another day. I think we call this Darwinism. If teams are tied for second/third place there's a series of tiebreakers to resolve who moves on. But just two teams advance. (Oh! Now I understand the message of the Australian patriotic song "Advance, Australia Fair"! It's a song urging the Socceroos to move forward in the tournament! See how neatly all this fits together?)

So. Question 6. What is the greatest number of points a team can get in the first round and FAIL TO ADVANCE? (Yes, it involves losing a tiebreaker.)

And Question 7. How about the least number of points a team can get in the first round and ADVANCE ANYWAY? (If you're reasoning by analogy from number 6, you might think again.)

Perhaps the most interesting challenge, though, is trying to reconstruct the individual results from the group standings. Surprisingly often, it can be done. Here's a current example. This is the UP TO THE MOMENT scoresheet for the four nations of Group G after each has played two games:

Country Points
Brazil 6
Portugal 4
Ivory Coast 1
N. Korea 0

Question 8: What were the four games already played, and how did they turn out?

(Spoiler alert.) Okay. If you've been paying attention you know that Brazil has 2 wins (3 + 3 = 6). Ivory Coast has a tie. North Korea has no points, so it's lost twice, and Portugal, with 4 points, must have a win (3 pts) and a tie (add 1 more). Now, follow along:

1. Brazil has only wins, but Portugal has no losses. Therefore Brazil hasn't played Portugal yet.

2. Since Brazil hasn't playd Portugal, then its two games were against North Korea and Ivory Coast.

3. Brazil won both of these games, since Brazil only has wins.

4. Portugal also has two games to be accounted for, and since the Portuguese haven't played Brazil they also must have played NK and IC.

5. Portugal has a win, which matches up nicely with North Korea's loss (the one that wasn't to Brazil);

6. and since Portugal and Ivory Coast are the only teams with ties, that game must have been a draw.

Therefore, the four games thus far:
Brazil over Ivory Coast
Brazil over North Korea
Portugal ties Ivory Coast
Portugal over North Korea
--Gimme a Q! Gimme an E! Gimme a D!

One more before I let you go. It's a bit tricky.

Question 9. WITHOUT LOOKING UP THE RESULTS, give the result AND THE FINAL SCORE of each of the four games played thus far by the teams of Group E.

Country Points Goals Scored Goals Allowed
Netherlands 6 3 0
Japan 3 1 1
Denmark 3 2 3
Cameroon 0 1 3

My friend Cheerful Charlie says the problem can't be solved, and he's (sort of) right; if you only look at the points column, you CAN'T tell who played (and beat) who. But if you look closely at the goals columns as well, you'll realize that there is a unique solution...one which, fortunately enough, happens to match reality. Good luck!

**Want answers? Want to know how you were supposed to know? Disagree with me and want me to (ahem) prove you're wrong? Fine. Send me an SASE containing your questions and comments and $1000 and... No, just email me at scurrie at-sign poughkeepsieday dot org and I'll be happy to respond. As soon as I'm done blaming France's troubles on the Slovakian equipment manager and a God-awful offsides call by a crooked linesman from Qatar, that is.**

When East Is West, and West Is East, and Ever the Twain Shall Meet

The current xkcd comic raises an interesting question.



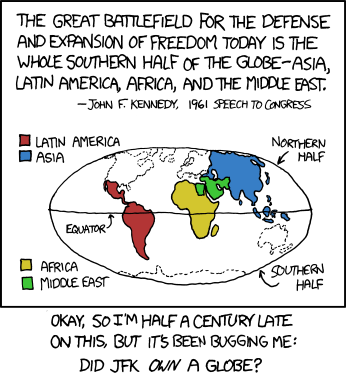
http://xkcd.com/753/

{Not that the non-JFKs among us are immune from this sort of thing. In the US alone:

+Large portions of West Virginia are actually east of much of Virginia, and some parts of Virginia are west-er than any part of "West" Virginia.

+Spartanburg, South Carolina is north of Wilmington, NORTH Carolina.

+The East River flows south as it makes its way through New York City, and the easternmost point in the continental US is called, what else, West Quoddy Head.

+South Bend is in extreme northern Indiana, West Bend a long way from anything we might call "western" Wisconsin, and for the fun of it I'll throw in the fact that Jo Daviess County in the northwestern corner of Illinois is traditionally lumped in with Carbondale, Decatur, and Cairo as part of the region known as "Downstate."

Okay, okay, I know there are reasons for all these names, North Carolina is (mostly) north of South Carolina, the East River is east (of Manhattan), Downstate Illinois basically means not-Chicago, yeah, yeah, yeah, what-ever. I still say we need truth in advertising. What's west should never be east, and what's down should not be up, and it should be possible to distinguish north from south easily and quickly and confidently. The spatial reasoning skills of our youngsters are at stake! Won't someone please think of the children?}

The Seven-Sided Hexagon; or, Epic Geometric Fail

So there I was in the local Rite Aid the other day, picking up grape juice and glue (don't ask), and my path toward these goodies took me down the Seasonal aisle. Where I discovered, much to my surprise, that though it was already early June the Back to School sales had not yet started and there was not a single Halloween mask anywhere in sight. (I wonder if the Home Office knows about this?)


More amazing still, I spotted a few assorted pieces of summer merchandise. Notably, a large box that contained a "Hexagonal Canopy." Which had a helpful explanatory diagram on the side of the box, for those who weren't quite sure what "hexagonal" meant:



Oops.

Birthday

"Know what?" crowed the little boy. "It's my birthday!"

"Congratulations!" I said. "How old are you now? Twelve?"

"Noooo!" he chortled. "I'm not twelve. I'm THIS much!" He held up four pudgy little four-year-old fingers.

"Oh, you're FOUR!" I said.

"Yeah!" he agreed.

"Congratulations," I said again. "Four is a very big number."

He went off to explain the situation to a few other adults, including some, like me, whom he knew reasonably well, and some whom he didn't know at all. "Know how old I am?" I heard again and again. "THIS much!" And out would go the four pudgy four-year-old fingers while the people--those who knew him and those who did not--reacted with appropriate surprise and astonishment.

When he'd finished working the room, he began all over again. "Guess what?" he said to me. "It's my birthday!"

"He's told me that three times already," remarked the teenager who was standing next to me.

"Well, it's very important news," I reminded her, and bent down, the better to talk to the birthday boy. "Congratulations," I said again.

"Do you know how old I am?" he demanded, and out went the four fingers: "I'm THIS many!"

"It certainly is a lot," I agreed.

"And do you know how old I was yesterday?" he asked.

An additional wrinkle. Fortunately, it sounded like a subtraction problem, and I'm pretty good at subtracting. I pondered. "You were three," I guessed.

He looked at me. He looked at his fingers. He looked at me again. A look of utter astonishment began to creep across his face.

"You're right!" he said. "But...how did you KNOW????"

Boys, Girls, and Paper Airplanes

PDS is on vacation this week, as many of you loyal readers know, but I am not on vacation exactly; among other things, my Vassar College course continues, and so I was in the classroom on Tuesday over at the Old Observatory.

As many of you loyal readers once again know, the class I'm teaching is Math and Science Methods, an elementary education course. We are now done with math (aww) and moving on to science. On Tuesday, we started with an interesting discussion about science education--the students' recollections of science, their associations with it, and so on.

A few notable highlights. On the whole these are relatively science-savvy students. One attended an elementary school near the Pacific Ocean in which the curriculum was based around marine science. Another had thoughts of going to medical school. A third took organic chemistry last fall--it's a notoriously hardcore science course, but one which she took (and I quote from the questionnaire I handed out at the beginning of the semester) "for fun." Others took AP Biology, have good memories of hunting for rocks, and so on. And when I asked them whether they had ever felt in any way that science was off-limits to them because of their gender (all the students enrolled in this class are women), they almost unanimously said they had not. I was pleased, if surprised. "That's very good to hear," I told them. "I don't know that the answer would've been the same in my generation."

And yet. A little later I asked them to tell me the first image that popped into their heads when I said a certain word. The word, you'll not be shocked to learn, was scientist. And here were the results. "My brother," said one student. "Bill Nye the Science Guy standing in a lab," said another. The rest all admitted to seeing a figure in a white coat in a laboratory. What kind of figure? Male or female? Male, they admitted, one after the other. Did anyone visualize a woman? I asked. Hesitation all around, then somewhat embarrassed shakes of the head. It may not have been the answer they wanted to give, but it was the truth: in this group of bright, well educated women, many of whom had a strong science background, all of whom attended a college that had a long history of empowering women and fighting stereotypes, every single one thought of a generic "scientist" as a male.

And one more thing. I'd assigned them to take some time to design two paper airplanes and bring them to class: one that would fly far, and one that would fly for a long time (distance for the first, duration aloft for the second). The purpose in part was to have them do the testing and questioning that's so central to science: what if I fold this wing up a bit more? what if I add some tape here? what throwing motion seems ideal? We would have a fly-off, I told them, after which valuable prizes (might) be awarded. (We did have the fly-off, by the way--see the picture below. The miserable weather cleared just enough to enable us to throw the planes off the balcony of the Old Observatory--one of the original buildings at Vassar and not so incidentally the building that served as the laboratory and office of the great astronomer Maria Mitchell, one of the finest scientists of her generation.)


Now, a comment here. I grew up making paper airplanes. I am sure I single-handedly destroyed dozens of trees in the process of making something that would fly, and fly well. (In my case I was less interested in distance than in duration aloft: the planes' ability to do loop-the-loops, arcs, and other tricks.) Most of my friends, as I look back, were into paper airplanes too. I don't remember girls getting involved much, if at all. Certainly my sister had little interest. Neither did my girl cousins. When I went on to become a classroom teacher, the trend continued. In nearly all my years at various grade levels, a group of kids started making whole fleets of paper airplanes at some point during the year. The group was almost always exclusively boys. Once in a while a girl would join in briefly, and was usually welcomed, but didn't stay for long. The only girls over the years who spent much time making and flying the planes were the few who usually sought out boys, rather than girls, as playmates. So I suspected that most of the young women in this college class had little experience with paper planes, and that's another reason why I assigned this as a task.

"So!" I said on Tuesday. "Did you enjoy the process?"

There was much grimacing and wrinkling of noses.

"I take it that means NO," I said. "How many of you spent much time as kids making paper airplanes?"

No hands went up. A few admitted that they had made an occasional plane, but added that their interest level had been low and their frustration level had been lower still. "Hmm," I said. "Now I wonder why that would be?"

One student raised her hand. "Paper airplanes are really a boy thing," she said, and then, realizing that we had once again stumbled into the tangled thicket of gender politics, added quickly, "I mean, I hate to stereotype, but..."

"No, no, go ahead," I said. "We're better off hearing the stereotypes than pretending they don't exist. We can always address them once they're on the table."

"All right," she said, nodding. "See, I went to these websites for information, and they were all, just, I don't know, written for boys. They were, like, 'Here's a great plane to throw at your teacher,' and I..." Her voice trailed off.

"And you never had the inclination to throw a plane at your teacher," I supplied. (Hoping it was true since I was a stationary target.)

"That's right," she said. "And one of the planes they said was best had directions, about 35 steps, and I got to about the twentieth step and it wasn't working, so..." She shrugged, leaving no doubt that while frustration might be a motivating force for some things, enduring all that agony for a $%^$% paper airplane wasn't worthwhile.

"I did the same thing," contributed another student. "I wanted to do my best, but it was so complicated and I found it really frustrating when I couldn't follow the directions. They even had a VIDEO on the website I looked at, and that didn't help either."

"Girls in my school didn't make paper airplanes," the young woman beside her remarked. "We made fortunetellers instead. You know, those things where you--" She pushed her fingers back and forth, miming the motion of turning a fortuneteller this way and that. "Boys sometimes used them," she added, "but the girls made them for the boys who wanted them."

"FORTUNETELLERS!!!" the rest of the class chorused, and then went off into a babble of individual conversations recalling the halcyon days of elementary school folding sessions. "Fortunetellers! They were so cool..." Evidently they had all made fortunetellers, and frequently at that. I, on the other hand, can't remember ever having made one. (I think I tried once and it was too frustrating. Hmm.)

"Yeah, it IS a boy thing," another student commented. "I showed my boyfriend the assignment and I didn't care all that much about it one way or the other, but he was SO EXCITED...."

So I suppose there's good news and bad news on the involving-girls-in-science front. These young women have good associations with science, mostly, and they believe they would be welcomed into the field if they were so inclined. Maria would be proud. Another piece of good news: science is about much more than paper airplanes. Now if we could only populate some of those stereotypically "scientific" white lab coats with women as well as with men...

Pentagon, Hexagon, Heptagon...

So there I was in the kindergarten, and the children were showing me how well versed they had become in the shapes of the pattern blocks (thanks, Robbie and Bill!).

"This shape has three sides," said Robbie, holding a triangle so the kids couldn't see it, and the children chorused "It's a triangle!"

"This shape has four sides, and they are all equal," she continued, and "Square!" shouted the class.

"And this one has six sides..." "Hexagon!"

"Oh, oh!" called out a little guy upon seeing the shape displayed (and yes indeed, it WAS a hexagon--phew!). "I know another shape! It's LIKE the hexagon! It's a--a--" He screwed up his face, thinking hard... "It's an OXagon!"

All I can tell you is, I would dearly love to see an oxagon in the wild. Wouldn't you?

The Goldilocks Method

We talk a lot about problemsolving strategies at PDS, especially in the 3rd-4th grades. One of the absolute favorites among the children is the one Icall the Goldilocks Method. Some texts refer to it as guess-and-check, or predict-and-test, but the name "Goldilocks Method" seems to have a greater "stickiness" quotient for kids.

The strategy is based, of course, on Goldilocks, Goldilocks of porridge fame, Goldilocks who could have been charged with breaking and entering, Goldilocks who encountered a trio of ursine forestdwellers...okay, okay, more to the point Goldilocks, who tasted the first bowl of porridge and found that it was TOO HOT, then tasted the second, which was TOO COLD, and finally tried the third, which was JUST RIGHT, and then repeated the process, replacing hot/cold with hard/soft and porridge with beds, but still coming out with JUST RIGHT at the end.

The students I'm working with in division right now used the Goldilocks Method the other day. They were playing a game to help them work with the connection between multiplication and division, and not so incidentally to practice mental math skills. I forget the name of the game (I usually do), but hey, grab a pencil, and you can play along with us at home:

First, choose a number between 600 and 800. No round numbers. (That is, no multiples of 10, like 790, 650, or 700. You will rarely hear me ban round numbers, but the fact is they're too easy to work with.)

Next, choose an odd number between 5 and 20.

Third, write a division expression with these numbers, such as "705 divided by 15."

The quotient will be--well, we don't know yet. But we can figure it out by using the Goldilocks Method. First, take the divisor (in this example, 15). Ask yourself: what do I have to multiply 15 by to get close to 705? We'll use a little mental math here: let's see, 10 x 15 is 150, so that's not close...20 x 15? Well, that would be 300. Okay, we're not getting there very quickly, so let's try 50 x 15. We'll write that down, calculate the product with either pencil-and-paper or a calculator, and discover that 50 x 15 = 750.

All right, what would Goldilocks say? She'd say TOO HOT. Or TOO HARD. Or TOO HIGH. Or something beginning with TOO. So, we need to try a smaller number. How about 45? Well, 45 x 15 = 675. TOO COLD/SOFT/LOW. Try something that's greater than 45. 48 x 15 = 720. Getting there! But still, TOO HIGH...

You see how this works. In this example, the original three-digit number was evenly divisible by 15, so it was possible to get something that was JUST RIGHT. Go, Goldilocks! Most of the time, it isn't possible in this game. That's okay too: we get as close as we can without going over, and then take the difference as the remainder. So for 696 divided by 9, we might say:

9 x 70 = 630 TOO LOW
9 x 80 = 720 TOO HIGH
9 x 75 = 675 TOO LOW
9 x 77 = 693 TOO LOW but oh-so-close...

And so our division sentence would be that 696 divided by 9 is 77, with a remainder of 3.

Goldilocks would be so proud...

From LOGO to Ladybugs

Early in my teaching career, PDS decided to provide each lower school classroom with a computer. Well, I should probably say "so-called computer," as the machine that graced my own classroom bore practically no resemblance to the current PDS fleet of laptops.

The machine, IIRC (and I'm sure I do RC), consisted of a keyboard, a monitor with a black-and-green screen, a separate drive for floppy disks (and floppy they were), and a whole mess of unnecessary wires. No mouse, no trackpad. No internet connection, no CD drive. No color, no sound. No bells, no whistles.

Oh, there was a printer of some description, a noisy and unreliable machine that routinely shredded the paper you fed it and printed letters better suited to connect-the-dots than to actual, you know, legibility.



The machine, which looked something like the one pictured above (minus the mouse), could do two things. The first was word processing, or what passed for it during the early-to-mid-eighties. The word processing was courtesy of a program called Bank Street Writer, which had been developed specifically for use in "educational settings." From where I sat it was hard to see why anyone had bothered. Bank Street Writer was clunky. It was slow. It was inefficient. It was practically useless. You had to use the keyboard arrows to select text for editing, which took forever, and they kept throwing the mid-eighties version of dialogue boxes at you when you did ("Are you sure you want to select this block of text? Y/N" "Are you REALLY sure? Y/N" "Are you positive? Y/N" "Are you sure you want to move it to the indicated place? Y/N" "Do you have any idea why we are asking all these questions? Y/N" "Don't you wish you'd decided to write this out longhand instead? Y/N.") Saving was a slow and frustrating process, as was retrieving previously-saved files. There was one difficult-to-read font (though there may have been two sizes, I'm not sure), and formatting was just about nonexistent. After a number of ol' college tries to find any way in which this program represented an improvement over almost anything else, I washed my hands of it and went back to the trusty old typewriter.



The other program was better. It was called LOGO, which was always written in capital letters though I'm not sure it actually stood for anything. LOGO allowed kids to do simple programming in a geometric context. You had what they called a turtle, which actually looked like a triangle but what the hey, and it sat there on the screen waiting to be told what to do. Kids could then type in various commands to make the turtle move. Typing in "BK 20," for instance, got the turtle to go 20 units in reverse (BK=backward, clever huh? and you thought it stood for Burger King). "FD 5" made it go forward 5 units. As it moved, it drew a line behind it. You couldn't make it go directly up or down, but you COULD make the turtle turn. Typing "RT 90" instructed it to spin 90 degrees to the right; "LT 135" got it to...well, you can figure it out.

There were lots of things to like about Logo, scuse me, LOGO. Kids had to type the directions using a specific format: if they typed "FD85" instead of "FD 85," the program would give them an error message. That made the children focus on precision--and helped demystify the computer and its abilities ("yup, it can do amazing things--but it CAN'T figure out what to do when it sees 'LT50' because NO ONE TOLD IT WHAT TO DO when someone mistypes something"). Kids very much enjoyed pretending to be the turtle and giving each other directions: "Okay, forward six steps..." The spatial reasoning aspect of LOGO was excellent--which way do I have to turn if I want to go straight up? what number do I need to input? And the use of left and right and the intro to angle measures were both valuable.

LOGO did have an issue. One goal of the software was to have kids program the turtle to make certain figures--squares, houses, and so on. Can you make a triangle? The letter Z? How? A few kids did get into this. Many, however, quickly decided that the REAL point of the program was to get the turtle to make random lines. We got lots of "FD 400" "FD 40" "FD 400" "FD 989"-style programs in which the turtle made a line to the right, disappeared off the right edge of the screen, came back on the left, and continued to do this for as many commands as the children had told it while the onlookers giggled. Another popular activity was to ignore the FD and BK commands in favor of having the turtle spin endlessly in place: LT 900, RT 42, LT 656, RT 851. Somebody figured out that if you told the turtle to make a turn of 1 unit before doing the FD commands, you could eventually have the turtle criss-cross the entire screen, effectively whiting it all out.

These were cute, and they required some thought at first (especially the white-out one), but once that initial thinking was over the activities quickly became kind of useless educationally. Kids weren't learning anything by repeatedly typing in BK 77 BK 77 BK 77, and the more they did that the less willing they seemed to want to engage in the actual making of shapes. There was something highly motivating about watching the turtle spin this way and that, and in contrast the work of plotting how to make a square seemed considerably less compelling. How you gonna keep 'em down on the farm, as the WWI song went, after they've seen Paree? Under these circumstances LOGO rapidly became less a tool for learning than a diversion for entertainment, and after a couple of years that began to sour me on the whole program. When "real" computers came along LOGO and its derivatives were not high on my list.

This year, though, I returned to my LOGO-ish roots. For our ongoing geometry unit in the 1-2 classes, we decided that I would pull kids during some of their math times and do some computer work. I'd pull out the laptops and work with kids on one or more of the virtual manipulatives at the Utah Sate University website: http://nlvm.usu.edu/. A lot of these materials are really excellent. Rods don't fall on the floor. Pattern block designs don't get wrecked when someone accidentally shakes the table. Virtual rubber bands don't break when you stretch them across a virtual geoboard. While not all materials on the site are equally great, many are quite wonderful.

But after looking through the various manipulatives on the site, I decided to focus on the most LOGOlike one: a program called Ladybug Leaf. (If you click on Geometry on the home page, it will be about 6 or 7 buttons down in the list.) The object of Ladybug Leaf is to direct a ladybug, LOGOstyle, to hide under a leaf. The graphics are far clearer and more engaging than they were in the old LOGO program. The ladybug is a real ladybug; the bug moves in clearly demarcated units; the leaf is a real leaf. The order of commands remains on the screen as the ladybug moves, with each command flashing briefly as the ladybug carries out that particular action. It's easy to replace a command, too--much easier than it used to be! True, FD 25 and LT 90 are things of the past in this activity, and I do kind of miss them. Instead, there are buttons you can click that will move the bug one unit forward or backward, or spin it 45 or 90 degrees to the left or the right. On the other hand, angle measures aren't exactly a staple of first and second grade mathematics, and you can always introduce the terms 45 and 90 degrees yourself.

Anyhow, the kids have been very much enjoying their venture into LOGOlike technology--and, I would like to think, learning important stuff along the way. It helps that in the last twenty-plus years I have learned a few things myself. In particular, I made sure to focus this time around on specific tasks: hide the bug under the leaf, move the leaf and hide it again, make a square, make a triangle, make a house (a house! See below, courtesy of one very thoughtful and dogged second grader)



There's nothing wrong with entertainment for its own sake, but I want a little more from, you know, school.

And how can I complain when that first grade girl who is ordinarily so reserved and so serious, after successfully planning a route to the leaf for her ladybug, celebrated by standing up and chanting "Oh yeah, oh yeah" while doing some disco moves?

Now if only someone could make some improvements to Bank Street Writer...

Blaming the Teacher

The world was better in the olden days. That's an article of faith among many Americans - and you will forgive me if I point out that it has been an article of faith for years and years and years. The "good ol' days" used to mean the period before World War I, or sometimes the 1920s. These days, though, the good ol' days have jumped forward to the fifties and the early sixties.

Ah, the Eisenhower/Kennedy years! A delightfully "innocent time," we read in Pete Hamill's review of the new book out about Willie Mays. A time when "anything and everything seemed possible," according to another book I recently ran across. A wonderful era when we had good old-fashioned values, when video games were nonexistent, when families ate dinner together every single night. Never mind the occasional problems: sexism, racism, McCarthyism, pollution, nuclear proliferation; it was the good ol' days, by golly, and everything was better back then.

As a teacher, I am especially tuned toward a particular mantra regarding the grandeur of the fifties/early sixties, which is that this era was the Golden Age of K-12 education. Everybody learned to read, quickly and easily. Everybody got really good at math. And in particular, the fifties-slash-early-sixties were a time when the education profession was respected, when parents and kids alike viewed teachers as professionals to be listened to and admired, not as lackeys to be walked all over and to be blamed for children's failures. Read the columns of child psychologist John Rosemond, just to name one strong proponent of this notion. Well, okay, I'll quote here from a typical Rosemond column, to save you the trouble of tracking them down yourself:

Back in the day, writes Rosemond, "when a child was reported to have made trouble in school, the child came home to even more trouble. Today, when a child is reported to have made trouble in school, the parents deny that the child is capable of making trouble, blame the teacher for having a 'personality conflict' with the child or failing to recognize the child's 'special needs' or 'boring' the child. In short, the school/teacher is in trouble."

Anyhow, I was reminded of this mantra while reading the Peanuts strip that appeared in the morning paper. I'm not sure how long this link will work, so I'll summarize the cartoon in addition to linking to it.

http://comics.com/peanuts/?DateAfter=2010-03-15&DateBefore=2010-03-15&Order=d.DateStrip+ASC&PerPage=1&x=7&y=8&Search=

Linus is distressed to find that he has failed to make the honor roll at school. Sweat pouring off his face and his wildish hair looking even more wild than usual, he tells Charlie Brown that he is "doomed," that his parents will be shocked and disappointed. (So far, so Rosemond.) Charlie Brown asks Linus what he thinks will happen, to which Linus replies, "Well, obviously, the first step will be to put in a complaint about the teacher."

The original publication date on the strip? March, 1963.

Oh. Okay. Perhaps things haven't changed as much as we thought.

Fathers, Sons, and Inequalities

I did a couple of days of Professional Development last week for a nearby school district. Hard work, but fun in its own way, and the teachers were very thoughtful and responsive, which was great. A few former colleagues of mine are working over there now, too, and it was wonderful to see them.

To illustrate some of my points about how children think about mathematics, I told some of my favorite stories, a few of which have appeared on this blog. But I left out this one, which took place in a kindergarten class early in my teaching career:

*****************

The little girl is almost always late being picked up. Her mother works till 3, and pickup is at 3, and the mother hasn't figured out how to be in two places at once. Technically I am supposed to send the girl to the After program if she hasn't been retrieved by 3:15, but the reality is that the After costs money, which the mom doesn't have much of. And besides, the mom is almost always there by 3:25. And anyway I'm an old softy at heart, or something.

So we have worked out a silent understanding, the girl and I. I go about my business in the classroom from 3 to the time she is picked up, tidying up and organizing the next day's work, and she sits quietly in the big rocking chair just outside the meeting corner rocking slowly back and forth, her lunch box by her side. Sometimes she looks at a book while she rocks. Other times she just rocks. It seems to be a nice decompression time for her. Once in a while we talk briefly, but she's never been much of a talker under any circumstances; so more often this is simply parallel play of a sort: the day is over, and she is in her world and I am in mine. When her mom arrives at 3:20 or 3:25, she slides out of the chair and heads for the door. "See you tomorrow," I say, but she is the strong, silent type, and so she smiles and wiggles her fingers at me in a half-mast wave, and then she is gone.

One day, though, another teacher stopped by my room at 3:20 to consult with me about something. The room was empty, of course, except for me and my late pickup, the girl in the rocking chair. I was taking clothespins off a bulletin board, if I remember correctly (and astonishingly, I think I do), and she was rocking, of course, the chair creaking as she meditatively swung back and forth.

The consultation finished, the teacher noticed that I was wearing a sweater (this was in the days when I still occasionally wore long sleeves). "Nice sweater," she said approvingly. "It looks handmade. Did someone make it for you?"

"Um," I said. "Well, sort of. My sister made it, knitted it for my father. But it turned out to be too small for him, so he passed it along to me."

The teacher nodded. "It seems to fit you just fine," she said, "and it's certainly striking," and with that she ducked back out of the room, and I returned to my clothespins to the accompaniment of the familiar, faint creak of the rocking chair--

When, quite suddenly and unexpectedly, the girl spoke up. "Your daddy is older than you are," she said.

I had almost forgotten she was in the room. Turning, I saw that she had a satisfied smile on her face. "Your daddy is older than you," she repeated, just in case I hadn't heard it the first time.

"Yes," I agreed. "That's right." Well, of course it was right. But I couldn't resist finding out the details of her thinking process. "What makes you say so?" I asked.

"The sweater was too small for your dad," she said proudly, her chair busily creaking as always, "but it fit YOU. So you are smaller than your dad. And if you're smaller than he is, then you must be younger, because people who are young are small." Creak, creak went the chair as she rocked harder and more enthusiastically. "So that means your dad has to be older than you."

What could I do but congratulate her on her remarkable reasoning ability? And it WAS impressive, even if entirely unnecessary, and this tiny little girl, not yet even six years old and still unwise in the ways of the world, deserved all the praise she could get. "You're absolutely right," I said, nodding my head slowly. "My dad IS older than me. You did a great job of figuring it out."

"Thanks," she said, taking the compliment as her due, and just then her mother walked in the door, and the girl slid off the rocker, exactly as she had done a few dozen times before, and she wiggled her fingers at me with a larger-than-usual smile. And though it's been probably twenty-five years since that incident, and though I lost track of that little girl long ago, I can still hear the creak of the rocking chair and see the self-satisfied grin on her face as she explained her impeccable logic...

Ah, memory. It's a funny thing.

Teaching Teachers to Teach

The "About Me" section in this blog states that I have worked with the education departments of a couple of local colleges. That's more true than ever this semester. With the usual instructor of Vassar's Math and Science Methods course on leave this spring, I have stepped into the breach and am now trying out being "Professor Currie" (that's ADJUNCT professor Currie to you--I'm not actually sure what my official title is).

I have a lovely class of what the education people like to call "preservice teachers," and so far the class is going well, and the students seem to be enjoying the activities and the discussions BUT there's a certain disconnection I'm noticing, which is that things seem pretty theoretical without, you know, actual children in the room. And teaching is all about children, right?



So for my most recent class I brought in a few children. Three, to be exact: three students who are currently fourth and fifth graders at PDS. The kids wandered in about 3:45 (class starts at 3:10) and sat down in too-big chairs in the seminar room. They looked a tad uncomfortable at first but soon warmed to the situation.



I started by asking them some questions about their enjoyment of math (they said they liked it, and a good thing too)--what they liked best about it ("it's challenging," a couple of them said), what was not so good ("when it's boring"--but I could've told you that in advance). I asked them to talk a little about how they learned multiplication as well. (Part of the focus of the class session was on multiplication and division.) Mathups, the kids agreed, had been very helpful, and using the array model had helped them understand the concepts too.



Other questions followed, both from me and from the students. What was your most memorable math project? (The corn kernels experiment, one student said. See the blog entries from October 2009 for more details on this one.) Do you prefer mental math or pencil and paper? Why? I had asked the college students to write an explanation of why the multiplication algorithm worked; one of the students was a bit unclear about one part and asked if the kids could explain it more clearly; one was happy to rise to the challenge. What manipulatives did they like? (NOT the pattern blocks, one child explained, adding "I like numbers best.") The kids were poised and articulate and knowledgeable, which was great to see. ("My, you know a lot!" I was tempted to say at one point. "Your math teacher must be HIGHLY skilled and no doubt deserves a medal and a large cash prize!" But I resisted.)



Finally, I'd arranged for the kids to teach the students a few multiplication games they had played in the past to help them learn and practice multiplication. So we divided into small groups, each with a child in charge, and off we went! The kids really enjoyed the chance to be in charge and the experts, and took well to the role.



We could've gone all afternoon, I think, but homework and other obligations loomed for the younger ones and us older ones had more discussion to do--so I paid the kids with some Freihofer's and thanked them much and off they went.



So the kids enjoyed it, and the students enjoyed it, and I enjoyed it, and it was an excellent reminder that teaching math involves teaching actual children. Fun stuff!

Obi-Wan, Mini Hot Dogs, and the Ninety-Dollar Jar of Olives

Hungry? You’ve come to the right place. Some of our second graders have been spending a few of their math periods lately planning menus for a special dinner. If they have leftovers (and judging from the amount of food some of them are planning to buy they’ll have lots), I’m sure they’d love to have you drop by.

Each of the children was instructed first to draw up a guest list consisting of seven fictional characters they’d like to get to know better. Their lists skewed heavily toward fantasy fiction: Lord of the Rings, Harry Potter, the Star Wars crowd. Obi-Wan Kenobi, in particular, will be kept busy nearly every evening for a week with invitations to these foodfests.



Next, they sketched out seating arrangements. One child set up four tables of two people each. Another planned for two tables, each seating four. Someone else constructed an octagon. (Eight people? Yes--seven guests and a host.) Then they planned a menu. “Not just desserts,” I cautioned them when it seemed clear that this was the way the wind was blowing. “A main course, or even two, so people can have a choice. An appetizer, perhaps. Soup, salad. Fruits and vegetables. Drinks.” “Oh, okay,” they said, and proceeded to put together menus that were...well, idiosyncratic, or what else would you call it when red snapper and turkey are served side by side?

Now came the most mathematical part: shopping. We did this in the comfort of our own classroom, using grocery ads from newspaper inserts as well as the circulars that arrived in my mailbox over time. I gave the children record sheets as well. “Find the items you want to buy,” I told them. “Record what the item is and how much it costs to buy just one. Then decide how many of the item you need. What will the total cost be? Figure that out and record it here in this column; then round that to the nearest whole dollar to make estimating the grand total easier.”

The children fell eagerly to work. “Mini hot dogs, mini hot dogs,” one boy repeated over and over, scanning the ads in vain for his favorite entrée. “Pizza!” crowed a classmate, jabbing a pencil at a listing in the frozen foods section of one advertising supplement. “Pizza?” asked a classmate. “Hey, I need that too!”



The kids needed help deciphering some of the prices: supermarkets, we learned, don’t often write prices the way teachers say you should. Instead of $1.59, for instance, they often write a big 1 followed by a smaller 59 and no decimal point or dollar sign at all: “Looks like a hundred and fifty-nine dollars,” one child said disapprovingly. “5 for $2” was confusing enough, but “4/3” to mean “you can get four for three dollars” was enough to make strong second graders cry. (Well, not literally. They were good sports about it and chalked it up as yet another example of the weirdness of adults.)

Determining how many of each item they needed was again idiosyncratic. One child decided that each person would probably eat 5 cookies, no, make that 6, so he settled on 48 as the number to buy. Somebody else, less generous or perhaps expecting that everyone would be full when dessert came around, decided to purchase just one small apple pie for the table. Did you need one carton of orange juice, or were you better off with 10? Different kids answered similar questions in wildly different ways.



Determining the cost of n cartons of orange juice, when n was more than 1, was often tricky as well. Some of these hosts have a beginning knowledge of multiplication, which they used to good effect. “Each cookie costs ten cents,” mused our 48-cookie-buying friend from before, “so 48 of them would cost, um, $4.80.” One child bought two jugs of milk at $2.99 apiece, set up the costs in columns, and laboriously regrouped to arrive at the total, $5.98; another, trying to determine the cost of two $4.98 items, rounded up to $5 for each, added the estimates to get to $10, and finally subtracted the extra four cents for a total of $9.96. We shared strategies and tried out newer, more efficient ones.




What about items that appeared on menus but were nowhere to be found in the ads? I hear you ask. Surely there were some of those. There were indeed, the aforementioned red snapper and mini hot dogs were among them. “Not a problem,” I said. “You have an idea of what similar things cost. Estimate the price. Just put a circle around the price on your record sheet to indicate that it’s an estimate.” Some estimates were IMHO pretty good. Others were...well, one cent for salad dressing was perhaps overly optimistic, and over $100 for a few other items seemed a tad excessive, but hey, who am I to complain?



Once the estimates were done, it was time to find a grand total. Making an estimate (using the rounded-to-the-nearest-dollar figures on the shopping list) was a job for mental arithmetic. Finding the actual total was a job for a calculator. Children compared the answers to make sure their totals were reasonable, then looked again at the total bill.

At first each was flabbergasted by the high cost of groceries (especially given the $90 jar of olives one of them purchased--an estimate, natch), but after a moment flabbergast vanished to be replaced by pride. Yes, indeed, they seemed to be saying, a meal that costs over $500 must certainly be something special. Now if only they’d found more expensive broccoli and purchased twelve loaves of bread instead of just two--

So the menus are done, the shopping lists are ready to go, and all that remains is to check on the availability of the guests. Anyone know if Dumbledore is free the evening of the 23rd? The invitation says six pm sharp, but he can arrive at seven if he doesn’t mind missing the goldfish and gummiworms being served as appetizers...

The Pirates of Poughkeepsie

It was Pirate Day in the 1-2s a little while back (arr!), and the buccaneers were out in force. Their captains, um, teachers, had a number of activities planned for them. One of these was locating a treasure chest that pirates of a previous era had buried somewhere in the Chapman Room. Luckily, these modern pirates had an appropriately antique map and faded directions.



“What’s it say next?” one pirate asked.

“Turn left,” another replied, squinting at the directions, and as one they all turned right.

“No, no, the other left,” their teacher explained helpfully.

They rotated 180° to the proper orientation. “Next,” said someone, “it says to take ten steps forward.” and they all took ten steps forward except for those who took twelve or thirteen because if ten steps are good then twelve or thirteen are even better, besides which if you’re the pirate in the lead you might get a bigger share of the treasure if and when it appears.



“Ten steps,” suggested the teacher....

So there they were, these young terrors-of-the-seas, thinking they were engaged in a search for hidden booty. But how wrong they were! Us Math Guy types knew the truth: They were actually engaged in Spatial Reasoning. Left, right, forward, backward, mapping, following directions, the whole nine yards. Proving that even pirates are mathematicians at heart--scuse me, at h(arr!)t.

Camera Shy

For those of you loyal readers who don't know what I look like, well, wonder no more! Though photographs of me are hard to come by on the web, a student kindly sketched my picture on the whiteboard that lives in the Chapman Room. Thanks to the miracles of modern technology, I can get you that image faster than you can say "Jackie Robinson." Here you go:



Thank you, Joanna in the 3-4 for the extremely accurate likeness (well, not quite; I am not nearly that handsome, but never mind). In any case, if you ever run into someone who looks almost exactly like that picture, you will know it must be me.

Cheerful Charlie and the Cupcakes

My good friend Cheerful Charlie, I told the third and fourth graders, was having a party, at which he planned to serve cupcakes. One hundred cupcakes, to be precise. I'm not sure who-all is on his guest list (other than me, of course), but he's either inviting a lot of people, or a few big eaters, or else he just wants a lot of leftovers.

Cheerful had (wisely) decided not to make these cupcakes from scratch (his measuring skills aren't what you would call real accurate), but was having some trouble determining which store he should go to. He had three choices, I explained, and he wanted to spend as little money as he could and get as good a deal as possible, and if the students could advise him that'd be great.

So, there was Cupcakes R Us, I told the kids, which sold baskets of 50 cupcakes at a shot, and each basket cost $40 but he also had to pay a fee of $5 to park.

And there was Cupcake Depot, where cupcakes were $9 per bag for a bag of 10, plus which Cheerful had a coupon for $5 off his total purchase.

And there was Cupcake's Discount Warehouse...

Look at all the information, I told them, and do some calculations if you need to, and decide if there are other considerations Cheerful should be thinking about, and then write Cheerful a letter suggesting what he ought to do. The students could turn in a handwritten letter which we'd forward on to Mr. Charlie, I explained, or they could email him directly at cheerful.charlie@yahoo.com, an account which he checks but not as regularly as he should because he often forgets or mistypes the password.

For some students, the assignment was just a relatively straightforward problem in arithmetic. You determine how many bags, boxes, or baskets of cupcakes Cheerful needs to buy at each store so he has 100 cupcakes in all; you multiply that number by the cost per box/bag/bucket/basket; you add the parking fee or membership fee, you subtract the coupon...and if you've done it right, you inform Cheerful that the cost at all three stores is the same, eighty-five bucks, and he can go wherever he likes and it doesn't make any difference. And this is a fine way of looking at it.

But what makes the problem interesting is the real-world nature of it. Sure, price is important. But is the lowest price always the best deal? I remember when my wife and I discovered WHY generic spaghetti sauce was so cheap (hint: it contained mostly water)... So the question becomes, what other things should Cheerful be taking into account?

Well, a lot of kids came up with lots of ideas.

"You should go to Cupcake's Discount Warehouse," one student wrote. The membership fee of $5 was annoying, she pointed out, "but if you have to go back again you will have your membership card so it'll be cheaper."

"Maybe you can walk to Cupcakes R Us," said somebody else. "Or ride a bike. Then you might not have to pay to park." (Note the "might." Hedging your bets, we call it.)

"It depends," wrote another student. "How far away are the stores?" A good question. If the nearest Cupcakes R Us outlet is in Albany, Scranton, or Paramus, it isn't worth the time and the gas to get there.

"You should ask them each for a free sample," suggested one optimist. "If you say you'll buy a lot they'll probably let you have one. Buy the one that tastes best." Not much point in saving five dollars if the cheaper cupcakes tasted like sawdust or carbon paper. --Or were made primarily of water, like the generic spaghetti sauce referred to above.

"Buy them in bags of 10," someone else advised. "The prices are all the same but if you need more then you only have to buy 10 more, not 20 or 25 or 50, and that will save you money."

And another student went right to the heart of the matter: Measure the cupcakes. "Buy the ones that are biggest," he suggested.

Unfortunately, Cheerful (who likes things simple) is still uncertain what to do: he's definitely bummed at the prospect of needing to find more information. We'll keep you posted. In the meantime, it was nice to see how many students recognized that there might be other considerations besides the cost of the cupcakes. We like to remind kids that math is about real-world situations, and in particular we like to point out that answers may not be as cut and dried as the textbooks sometimes suggest they are. This was a good example of both--and a good example of how a little knowledge can be a dangerous thing.

(Though regarding "other considerations," you CAN have too much of a good thing: see one of my favorite cartoons of all time, http://xkcd.com/309/. --Cut and paste the URL into your browser window if the link doesn't work for you. The two folks on the extreme right? That would be me and my wife...)

Sleepovers

(Warning: This is not about math.)

Back when I was a classroom teacher, I once taught a girl we will call Claudia. Claudia was new to the school and was a member of my 1-2 class. She was shy and quiet, but she took school seriously and was quite eager to please.

Writing skills are of course a major part of the 1-2 curriculum. Most children try out different subjects and themes as they are learning to write. Not Claudia. Her first three pieces of writing were all essentially the same. Allowing for some variation in wording and the name of her host, they all read like this:

"I slept over my friend Kari's house. First we played. Then we ate dinner. After that we watched TV. Then we played some more. We went to bed. In the morning we had breakfast. Then we watched TV. We played. Then I went home."

At first, I simply worked with Claudia to improve her writing given this basic framework. Could she add some details? What show did she watch, what did she have for dinner? How about putting in some describing words? Was the bed hard or soft, was the TV show funny or scary? I offered some ideas for varying the sentence structure and helped her explore other ways to organize the information. "Conferencing," we call it (though I'm not sure we called it "conferencing" back in the day), and Claudia dutifully added the information I told her to include, and each of the first three stories wound up a little bit different in final form, though not, I must admit, a lot different.

Perhaps, for deep psychological reasons, it was very necessary for Claudia to tell this same story again and again, but where her writing was concerned the constant repetition seemed to be getting in her way. Ideas, after all, were important too. I decided that the "Claudia and the Sleepover" series, Vols 1-3, was borne less of emotional turmoil and more of being in a rut. So when it came time for her to start her next piece of writing, I called her aside.

"You've been writing a lot about your sleepovers," I told her. "I know you like writing those stories, but I think you're ready to write about something new. Let's try this. What's the weirdest, strangest, most unbelievable thing you can think of?"

Claudia thought for a moment. "You mean," she said slowly, "like, my stuffed animals came to life?"

This was a greater leap than I had expected--a highly imaginative response, and given almost immediately. YES!! I thought. "Sounds great," I said, smiling. "So, here's your first line: 'Last night my stuffed animals came to life!' Got it?"

Claudia nodded.

"Then go get 'em," I said, steering her back to her seat. She picked up her pencil and started writing. Excellent, I thought as I moved off to consult with the next child. I'd said the right thing at the right time. I'd handled Claudia well; I'd started her down the road toward more creativity and a greater interest in writing. This was why the school paid me the big bucks. (So to speak).

That warm glow lasted only ten minutes, however, because when I returned to check in with Claudia this is what she had written on her paper:

"Last night my stuffed animals came to life. And they had a sleepover. First, they played..."

A PalindromemordnilaP A

John McAdam, professor of education at Marist College and a fellow Math Guy in spirit if not in title, reminds me that today is a palindrome: when written in month/day/year format, the digits are the same read forward as read backward:

01/02/2010

Okay, okay, you have to put a couple of leading zeroes in there, but pretty darn good, wouldn't you say?

And FYI, the next one will be 11/02/2011. A loooong way off. So as Paul Simon (the singer not the senator) never put it,

enjoy it while you can, Nan
it ain't all that bad, Dad
there's no need to sob, Bob
just sit down and chill, Lil
and eat a banana, Hannah
(or some other food, Dood)
Just leave it to me... .